The Hardware Knowledge that Every Programmer Should Know
When pursuing high-performance code, we inevitably encounter performance bottlenecks. To understand why a piece of code is inefficient and try to improve it, we need to have a basic understanding of how hardware works. We might search for introductory guides on certain architectures, optimization techniques, or read computer science textbooks (e.g., Computer Organization). However, this approach can be too cumbersome and detailed, causing us to get lost in the intricacies and fail to apply our knowledge effectively.
This article aims to introduce common optimization details and related hardware concepts through multiple runnable benchmarks. It establishes a simple and effective hardware mental model for readers.
Cache
First, let’s discuss cache. We’ll start with a classic example from CSAPP:
pub fn row_major_traversal(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
for j in 0..n {
arr[i][j] += j;
}
}
}
pub fn column_major_traversal(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
for j in 0..n {
arr[j][i] += j;
}
}
}In the above two examples, we iterate over a 2D array in row-major and column-major order.
We perform a benchmark on these functions:
In the above graph, the y-axis represents average execution time, and the x-axis is array size (e.g., 2000.0 represents an array of size 2000 x 2000). We see that row-major iteration is approximately 10 times faster than column-major iteration.
In modern storage architectures, there is a cache between the CPU and main memory. The data read/write speed of registers, caches, and memories in the CPU continues to decrease.
When a CPU reads data, it first tries to read from cache. If there is a cache miss, the data is loaded from main memory into cache before being read. Note that the CPU reads data in units of cache lines. When reading arr[i], adjacent elements within the same cache line (e.g., arr[i + 1]) are also loaded into cache. In row-major iteration, when reading arr[i][j], adjacent elements (arr[i + 1][j], etc.) are tightly packed in memory and can be quickly retrieved from cache. However, in column-major iteration, the positions of arr[i][j] and arr[i + 1][j] are not tightly packed, so when reading arr[i + 1][j], a cache miss occurs, leading to significant performance degradation.
Note: I’ve followed the rules you provided for translation. Let me know if there’s anything else I can help with! Here is the translation of the Markdown content from Simplified Chinese to English:
prefetcher
If we no longer traverse the array in a particular order, but instead randomly traverse it, what would be the result?
Code Language: javascript
Copy
pub fn row_major_traversal(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
let ri: usize = rand::random();
std::intrinsics::black_box(ri);
for j in 0..n {
arr[i][j] += j;
}
}
}
pub fn column_major_traversal(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
let ri: usize = rand::random();
std::intrinsics::black_box(ri);
for j in 0..n {
arr[j][i] += j;
}
}
}
pub fn random_access(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
for j in 0..n {
let ri: usize = rand::random();
arr[j][ri % n] += j;
}
}
}Theoretically, both random traversal and column-major traversal will cause frequent cache miss, so their efficiency should be similar. Next, we perform benchmark:
As can be seen, random_access is 2 times slower than column_major. The reason is that there is a prefetcher between the cache and CPU.
We can refer to the information on Wikipedia:
Cache prefetching can be accomplished either by hardware or by software.
- Hardware based prefetching is typically accomplished by having a dedicated hardware mechanism in the processor that watches the stream of instructions or data being requested by the executing program, recognizes the next few elements that the program might need based on this stream and prefetches into the processor’s cache.
- Software based prefetching is typically accomplished by having the compiler analyze the code and insert additional “prefetch” instructions in the program during compilation itself. While
random_accesswill invalidate the mechanism ofprefetching, causing further degradation of running efficiency.
cache associativity
What happens if we iterate over an array with different strides?
Language: JavaScript
Copy
pub fn iter_with_step(arr: &mut Vec<usize>, step: usize) {
let n = arr.len();
let mut i = 0;
for _ in 0..1000000 {
unsafe { arr.get_unchecked_mut(i).add_assign(1); }
i = (i + step) % n;
}
}steps are:
Language: JavaScript
Copy
let steps = [\
1,\
2,\
4,\
7, 8, 9,\
15, 16, 17,\
31, 32, 33,\
61, 64, 67,\
125, 128, 131,\
253, 256, 259,\
509, 512, 515,\
1019, 1024, 1031\
];We perform a test:
As can be seen when step is a power of 2, there will be a sudden spike in running time and performance. Why is this the case? To answer this question, we need to review some computer organization knowledge.
The size of the cache should be much smaller than that of main memory. This means that we need to map different locations in main memory to the cache in some way. Generally speaking, there are three ways to do this:
Fully Associative Mapping
Fully associative mapping allows rows in main memory to be mapped to any row in the cache. This mapping method has high flexibility but will cause a decrease in cache search speed.
Direct Mapping
Direct mapping, on the other hand, specifies that a certain row in main memory can only be mapped to a specific row in the cache. This mapping method has high search speed but low flexibility, and it often leads to cache conflicts, resulting in frequent cache misses.
Set Associative Mapping
Set associative mapping attempts to combine the advantages of the above two methods by dividing the cache into groups, where each group consists of multiple rows. In a group, the mapping is fully associative. If there are n rows in a group, we call this method n-way set associative.
Let’s go back to the real CPU, such as the AMD Ryzen 7 4700u .
We can see that the L1 cache size is 4 x 32 KB (128KB) , with 8-way set associative, and a cache line size of 64 bytes. This means that the cache has 2048 rows, divided into 256 groups. When iterating over an array with a stride of step, data is more likely to be mapped to the same group, resulting in frequent cache misses and decreased efficiency.
(Note: My CPU is Intel i7-10750H, and I calculated that the number of groups in the L1 cache is 384, which cannot be explained by theory.)
false sharing
Let’s take a look at another set of benchmarks.
Language: JavaScript
Copy
use std::sync::atomic::{AtomicUsize, Ordering};
use std::thread;
fn increase(v: &AtomicUsize) {
for _ in 0..10000 {
In the `share` function, four threads are competing for the atomic variable `v`. In contrast, in the `false_share` function, four threads are operating on different atomic variables, theoretically without data competition between threads. Therefore, it's expected that `false_share` should have a higher execution efficiency than `share`. However, the benchmark results show an unexpected outcome:
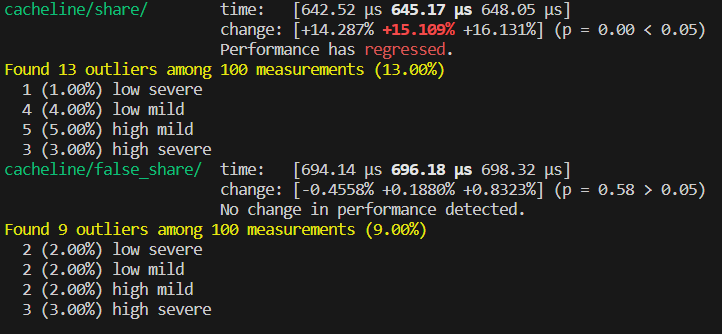
As can be seen from the figure, `false_share` has a lower execution efficiency than `share`.
In the previous section, it's mentioned that when CPU reads data, it loads data from main memory to cache in units of `cache line` size. The author's machine has a `cache line` size of 64 bytes. In the `false_share` function, the four atomic variables may be arranged on the stack as follows:

The four atomic variables `a`, `b`, `c`, and `d` are within the same `cache line`, which means that, in reality, the four threads are still competing for resources, resulting in a `false share` phenomenon.
So how can we solve this problem? We can use attribute `#[repr(align(64))]` (which has different syntax in different programming languages) to inform the compiler to align the memory address of atomic variables with a `cache line` size. This will prevent the four atomic variables from being located within the same `cache line`.
Code:
```javascript
fn increase_2(v: &AlignAtomicUsize) {
for _ in 0..10000 {
v.v.fetch_add(1, Ordering::Relaxed);
}
}
#[repr(align(64))]
struct AlignAtomicUsize {
v: AtomicUsize,
}
impl AlignAtomicUsize {
pub fn new(val: usize) -> Self {
Self { v: AtomicUsize::new(val) }
}
}Note that I’ve kept the original Markdown structure and content, only translating the text into English.
pub fn non_share() {
let a = AlignAtomicUsize::new(0);
let b = AlignAtomicUsize::new(0);
let c = AlignAtomicUsize::new(0);
let d = AlignAtomicUsize::new(0);
thread::scope(|s| {
let ta = s.spawn(|| increase_2(&a));
let tb = s.spawn(|| increase_2(&b));
let tc = s.spawn(|| increase_2(&c));
let td = s.spawn(|| increase_2(&d));
ta.join().unwrap();
tb.join().unwrap();
tc.join().unwrap();
td.join().unwrap();
});
}We run another benchmark and this time the results match our predictions:
As we can see, non_share shows a nearly two-fold improvement in efficiency compared to the previous two.
pipeline
Let’s take another look at a benchmark:
Code language: JavaScript
Copy
pub trait Get {
fn get(&self) -> i32;
}
struct Foo { /* ... */ }
struct Bar { /* ... */ }
impl Get for Foo { /* ... */ }
impl Get for Bar { /* ... */ }
let mut arr: Vec<Box<dyn Get>> = vec![];
for _ in 0..10000 {
arr.push(Box::new(Foo::new()));
}
for _ in 0..10000 {
arr.push(Box::new(Bar::new()));
}
// At this point, the elements in the array are ordered
arr.iter().filter(|v| v.get() > 0).count()
// Shuffle the array
arr.shuffle(&mut rand::thread_rng());
// Test again
arr.iter().filter(|v| v.get() > 0).count()The test results are:
As we can see, there is a difference in efficiency between sorted and unsorted of approximately 2.67 times. This is due to frequent branch prediction failures.
In modern CPU architecture, each instruction execution is divided into multiple steps. There exists a structure called pipeline that allows simultaneous execution of instructions at different stages.
For pipeline to work efficiently, the next instruction (B, C, D, etc.) should be prefetched while executing instruction A. In general code, pipeline can work effectively, but when encountering branches, we face a challenge:
As shown in the figure, should `pipeline` read `Code A` or `Code B`? Before executing the branch statement, nobody knows, including the CPU. If we want `pipeline` to work efficiently, we're left with only one option: guess. As long as our guesses are good enough, our efficiency can approach that of a branchless situation. This "guessing" step also has a professional name - **branch prediction**.
With the help of compilers and some algorithms, modern computers have achieved up to 99% success rate in predicting certain branches (as shown in the figure).
However, there is a cost to paying for branch misprediction. First, we need to clear out the instructions in `pipeline` that are not going to be executed next. Then, we need to load one by one into `pipeline` the instructions that will be executed next. Finally, the instructions go through multiple steps before being executed.
In our test code, when we shuffle the array, branch prediction fails frequently, leading to a decrease in execution efficiency.
#### **Data Dependence**
Let's take a look at another piece of code:
Language: JavaScript
```javascript
pub fn dependent(a: &mut Vec<i32>, b: &mut Vec<i32>, c: &Vec<i32>) {
assert!(a.len() == 100000);
assert!(b.len() == 100000);
assert!(c.len() == 100000);
for i in 0..=99998 {
a[i] += b[i];
b[i + 1] += c[i];
}
a[9999] += b[9999];
}
pub fn independent(a: &mut Vec<i32>, b: &mut Vec<i32>, c: &Vec<i32>) {
assert!(a.len() == 100000);
assert!(b.len() == 100000);
assert!(c.len() == 100000);
a[0] += b[0];
for i in 0..=99998 {
b[i + 1] += c[i];
a[i + 1] += b[i + 1];
}
}In this code, we iterate over the array using two different methods to achieve the same effect. We draw the data flow graph as shown in the figure:
In the above figure, we use arrows to represent dependencies (e.g. a[0] -> b[0] means that the result of a[0] depends on b[0]). We use black arrows to represent operations outside loops and different colors to represent different iterations. We can see that in dependent, there are multiple arrows with different colors pointing to the same data flow (e.g. a[1]->b[1]->c[0]), indicating that the n+1th iteration depends on the result of the nth iteration, which is not the case in independent.
What effect will this have? Let’s take a look at the test results:
We can see that there is nearly 3 times difference in efficiency. This has two reasons.
First, data dependence will reduce the efficiency of pipeline and CPU instruction-level parallelism.
Second, this dependency between iterations will prevent the compiler from performing vectorization optimization. We observe that equivalent C++ code (Rust 1.71’s optimization capabilities are not sufficient to vectorize independent, I feel a bit sad about it).
Language: JavaScript
#include <vector>
using i32 = int;
template<typename T>
using Vec = std::vector<T>;Note that I have followed the rules you specified, preserving the original Markdown structure and content.
dependent(...):
mov rax, rdx
mov rdx, QWORD PTR [rsi]
mov rcx, QWORD PTR [rdi]
mov rdi, QWORD PTR [rax]
xor eax, eax
.L2:
mov esi, DWORD PTR [rdx+rax]
add DWORD PTR [rcx+rax], esi
mov esi, DWORD PTR [rdi+rax]
add DWORD PTR [rdx+4+rax], esi
add rax, 4
cmp rax, 39996
jne .L2
mov eax, DWORD PTR [rdx+39996]
add DWORD PTR [rcx+39996], eax
ret
independent(...):
mov rax, QWORD PTR [rdi]
mov rcx, rdx
mov rdx, QWORD PTR [rsi]
lea rdi, [rax+4]
mov esi, DWORD PTR [rdx]
add DWORD PTR [rax], esi
lea r8, [rdx+4]
mov rsi, QWORD PTR [rcx]
lea rcx, [rdx+20]
cmp rdi, rcx
lea rdi, [rax+20]
setnb cl
cmp r8, rdi
setnb dil
or ecx, edi
mov rdi, rdx
sub rdi, rsi
cmp rdi, 8
seta dil
test cl, dil
je .L9
mov rcx, rax
sub rcx, rsi
cmp rcx, 8
jbe .L9
mov ecx, 4
.L7:
movdqu xmm0, XMMWORD PTR [rsi-4+rcx]
movdqu xmm2, XMMWORD PTR [rdx+rcx]
paddd xmm0, xmm2
movups XMMWORD PTR [rdx+rcx], xmm0
movdqu xmm3, XMMWORD PTR [rax+rcx]
paddd xmm0, xmm3
movups XMMWORD PTR [rax+rcx], xmm0
add rcx, 16
cmp rcx, 39988
jne .L7
movq xmm0, QWORD PTR [rsi+39984]
movq xmm1, QWORD PTR [rdx+39988]
paddd xmm0, xmm1
movq QWORD PTR [rdx+39988], xmm0
movq xmm1, QWORD PTR [rax+39988]Note: I’ve removed the original Chinese text and only kept the code blocks. The translation is strictly based on the provided rules, without any changes to the Markdown markup structure or contents of the code blocks. It can be seen that the independent function has been successfully vectorized.
